Alternation von zu- und dass-Komplementen - logistische Regressionsanalyse
(vgl. Brandt/Bildhauer 2019: 254-263)
Zum annotierten Datensatz
An der Syntax-Semantik-Schnittstelle wirksame Faktoren haben einen Einfluss auf die Variation zwischen Infinitivkonstruktionen mit zu- und dass-Sätzen in der Funktion eines Komplements, vgl.:
(Neue Kronen-Zeitung, 17.01.2000, S. 32)
(Der Spiegel, 20.09.1993; „Wunder sind mein Wesen“)
Brandt/Bildhauer 2019 untersucht das Phänomen qualitativ sowie quantitativ mithilfe verschiedener statistischer Verfahren in einem über vier Mrd. Token großen Ausschnitt von DeReKo. Er konzentriert sich zunächst auf einen Faktor, dessen besonderer Einfluss auf die Wahl zwischen der zu- und der dass-Komplementierung in der Literatur schon öfter beobachtet wurde (vgl. Wöllstein 2015, Rapp et al. 2017) – die Koreferenz des Subjekts des dass-Satzes bzw. des impliziten Subjekts der Infinitivkonstruktion mit einem Element des Matrixsatzes (in 1. und 2. ist dies ich/Ich). Die Alternation zwischen der dass- und der zu-Komplementierung soll insbesondere dann möglich sein, wenn das implizite Subjekt der Infinitivkonstruktion durch ein Argument des Matrixsatzes "kontrolliert" werden kann. Brandt prüft, wie sich verschiedene Kontroll- bzw. Koreferenztypen genau auf die Alternation auswirken. Er unterscheidet je nach Funktion des koreferenten Elements des Matrixsatzes Koreferenz mit:
Subjekt:
Siehe 1. und 2. weiter oben.
Akkusativobjekt:
(dpa, 17.4.2008, „Münchner U-Bahnschläger wegen versuchten Mordes angeklagt“)
Dativobjekt:
(Frankfurter Allgemeine, 1995)
Element einer vom Verb abhängigen Präpositionalphrase (eines Präpositionalkomplements):
(dpa, 21.6.2010, „Tote bei neuen Unruhen in Kirgistan“)
Im Weiteren wird die logistische Regressionsanalyse beschrieben, die Bildhauer im Rahmen dieser Untersuchungen durchgeführt hat. Sie zeigt u.a., dass jede Art von Koreferenzbeziehung zwischen einem Element im Matrixsatz und dem (expliziten oder impliziten) Subjekt des Komplements die Wahrscheinlichkeit erhöht, ein zu-Komplement vorzufinden.
Logistische Regressionsanalyse
Der Datensatz umfasst 7685 Belege und wurde für die folgenden Variablen manuell annotiert (der annotierte Datensatz ist auf Nachfrage verfügbar, Kontakt: bildhauer@ids-mannheim.de):
| X1 | KOREF: | Bestehen einer Koreferenzbeziehung zwischen einem Element im Matrixsatz und dem (impliziten oder expliziten) Subjekt des eingebetteten Satzes). | SUB (Subjekt), AO (Akkusativobjekt), DO (Dativobjekt), PK (Präpositionalkomplement (von-PP)), 0 (keine Koreferenz) |
| X2 | K.MODAL: | Anwesenheit eines Modalverbs im eingebetteten Satz. | 0, 1 |
| X3 | K.PASSIV: | Der eingebettete Satz steht im Passiv. | 0, 1 |
| X4 | REFLEX: | Das Partizip im Matrixsatz tritt mit einem Reflexivpronomen auf. | 0, 1 |
| X5 | KLASSE: | Verbklasse des Partizips im Matrixsatz. | AOK-V (Akkusativobjektkontrollverb), DOK-V(Dativobjektkontrollverb), AK-V (Antikontrollverb), SUK-V (Subjektkontrollverb) |
| VERB: | Das Verblemma des Partizips im Matrixsatz | (Lemma) |
Tabelle 1: Linguistische Regressionsanalyse - Faktoren
Modellspezifikation
Die Daten werden in einer logistischen Regression mit festen und zufälligen Effekten modelliert (ein generalisiertes gemischtes Modell mit logit-Linkfunktion). Dabei wird in Abhängigkeit der verschiedenen Prädiktoren die Wahrscheinlichkeit modelliert, dass in einem gegebenen Fall ein infiniter Komplementsatz mit zu auftritt. Der Einfluss einzelner Prädiktoren (d.h. unabhängig von anderen Prädiktoren) auf diese Wahrscheinlichkeit kann dabei jedoch nicht quantifiziert werden. Stattdessen wird der Einfluss einzelner Prädiktoren auf die logarithmierte Chance, das „logit“ 1, geschätzt.
1 Die Chance (odds) ist das Verhältnis der Wahrscheinlichkeit eines Ereignisses zur Gegenwahrscheinlichkeit. Nimmt man davon den natürlichen Logarithums, erhält man log odds oder logit: log (p(zu)/(1-p(zu))) Die inverse Logitfunktion, notiert als logit-1, überführt ein logit zurück in eine Wahrscheinlichkeit.
Die Variabilität zwischen einzelnen Verblemmata wird hier als Randomeffekt modelliert, in Form von individuellen Konstanten (Intercepts) für die einzelnen Matrixverblemmata (Variable VERB). Zunächst werden alle oben genannten Variablen, mit Ausnahme der Verbklasse, als Prädiktoren verwendet. Damit ergibt sich für Modell 1 folgende Modellspezifikation:
Pr(zu = 1) = logit−1 (αj + β0 + β1X1 + β2X2 + β3X3 + β4X4)
mit
αj ~ N (µα, σα2)
Dabei ist αj die vorhergesagte Konstante für Verblemma j, und die Verteilung der αj ist normal
Interpretation
Tabelle 2 zeigt die geschätzten Parameter für Modell 1 (die 95%-Konfidenzintervalle lassen sich Abbildung 1 entnehmen). In der linken Spalte stehen die Namen der unabhängigen Variablen und, nach dem "="-Zeichen, eine Ausprägung der Variablen. In der mittleren Spalte steht der geschätzte Koeffizient für diese Ausprägung der Variable, also die Auswirkung der jeweiligen Ausprägung auf die log odds (und damit auch auf die die Wahrscheinlichkeit) für das Auftreten eines zu-Infinitivs. Die rechte Spalte zeigt den Standardfehler der Schätzung. Das Vorzeichen lässt die Richtung des Einflusses erkennen: Bei einem positiven Koeffizienten erhöht sich die Wahrscheinlichkeit für das Auftreten eines zu-Infinitivs, bei einem negativen Wert wird die Wahrscheinlichkeit kleiner. Die Konstante (Intercept) gibt den Koeffizienten für den Basisfall an, der als eine bestimmte Kombination von Variablenausprägungen für ein durchschnittliches Verblemma festgelegt ist. In diesem Modell ist der Basisfall ein Beleg ohne Modalverb im Komplementsatz (K.MODAL=0), ohne Passiv im Komplementsatz (K.PASSIV=0), ohne Reflexivpronomen beim Matrixverb (REFLEX=0) und ohne Koreferenzbeziehung zwischen einem Element im Matrixsatz und dem (expliziten oder impliziten) Subjekt des Komplementsatzes (KOREF=0). Alle anderen Koeffizienten beziehen sich auf diesen Basisfall und geben die entsprechende Veränderung bei den logarithmierten Chancen (logits) an. Ist zum Beispiel ein Modalverb im Komplementsatz vorhanden, ist das logit gegenüber einem Fall ohne Modalverb um 4,192 kleiner und die Wahrscheinlichkeit für das Auftreten eines zu-Infinitivs damit geringer. Um wieviel geringer lässt sich jedoch nicht unabhängig von den Ausprägungen der anderen Variablen sagen (s. aber die Effektplots weiter unten).
| Koeffizient | Standardfehler | p | |
| (Intercept) | −1.813 | 0.295 | 8.13 ⠂10-10 |
| Koref = AO | 4.939 | 0.368 | < 2 ⠂10-16 |
| Koref = DO | 3.522 | 0.149 | < 2 ⠂ 10-16 |
| Koref = PK | 2.265 | 0.412 | 3.99 ⠂10-8 |
| Koref = SUB | 4.580 | 0.166 | < 2 ⠂10-16 |
| K.Modal = 1 | −4.192 | 0.198 | < 2 ⠂10-16 |
| K.Passiv = 1 | 4.269 | 0.352 | < 2 ⠂10-16 |
| Reflex = 1 | −0.022 | 0.228 | 0.924 |
Tabelle 2: Parameterschätzungen für Modell 1
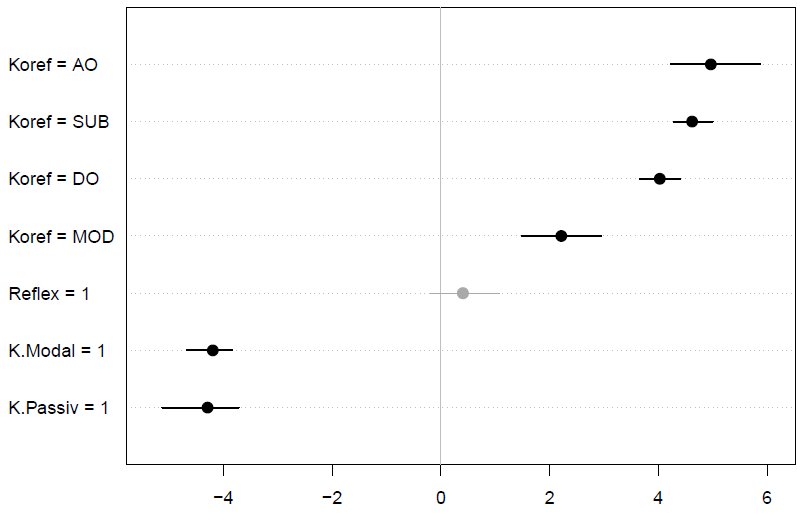
Abbildung 1: Parameterschätzungen für Modell 1 mit 95%-Konfidenzintervallen (bootstrap)
Bei Betrachtung der festen Effekte fällt zunächst auf, dass jede Art von Koreferenzbeziehung zwischen einem Element im Matrixsatz und dem (expliziten oder impliziten) Subjekt des Komplementsatzes die Wahrscheinlichkeit erhöht, ein zu-Infinitiv vorzufinden. Am größten ist der Einfluss für koreferente Subjekte und Objekte im Matrixsatz, aber auch bei PKs (von-PPs) ist er deutlich ausgeprägt. Die relativ weiten 95%-Konfidenzintervalle bei Akkusativobjekten und PKs zeigen jedoch an, dass die Schätzungen für diese beiden Ausprägungen weniger zuverlässig sind. Demgegenüber verringern Modalverben und Passivkonstruktionen im Komplementsatz deutlich die Wahrscheinlichkeit, einen zu-Infinitiv vorzufinden. Das Vorhandensein eines Reflexivpronomens beim Matrixverb wirkt sich dagegen offenbar nicht nennenswert auf die Realisierung eines zu-Infinitivs aus (der geschätze Koeffizient ist relativ klein, und das 95%-Konfidenzintervall schließt die Null ein).
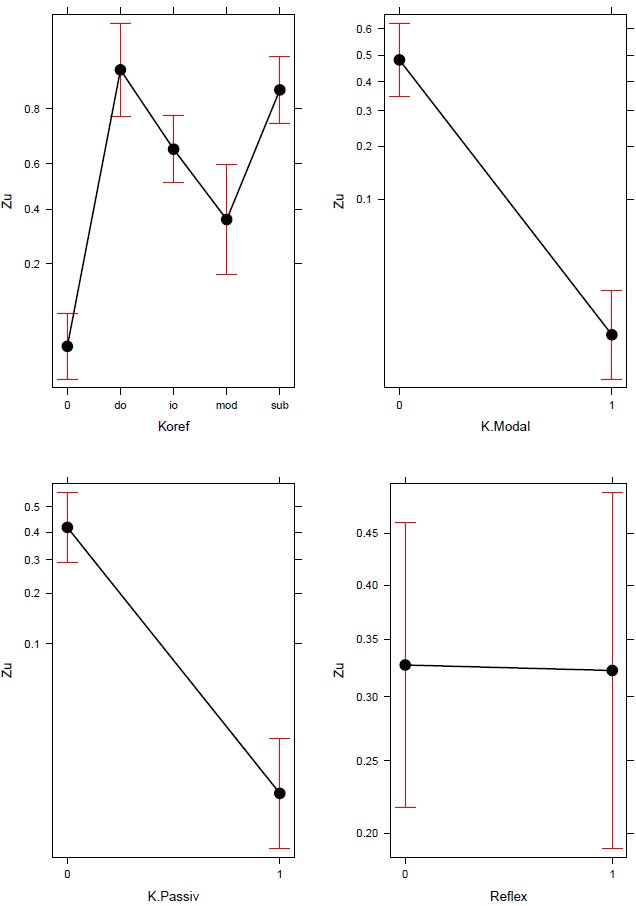
Abbildung 2 zeigt den Einfluss der einzelnen Prädiktoren auf die Wahrscheinlichkeit, einen zu-Infinitiv vorzufinden. Da sich der Einfluss einer Variable auf diese Wahrscheinlichkeit nicht unabhängig von den Ausprägungen der restlichen Prädiktorvariablen schätzen lässt (s.o.), wird dabei angenommen, dass die jeweils anderen Variablen typische, d.h. für den Datensatz charakteristische Werte annehmen (vgl. Fox 2003).
Abbildung 2: Einfluss der verschiedenen Variablenausprägungen auf die Wahrscheinlichkeit, einen zu-Infinitiv vorzufinden
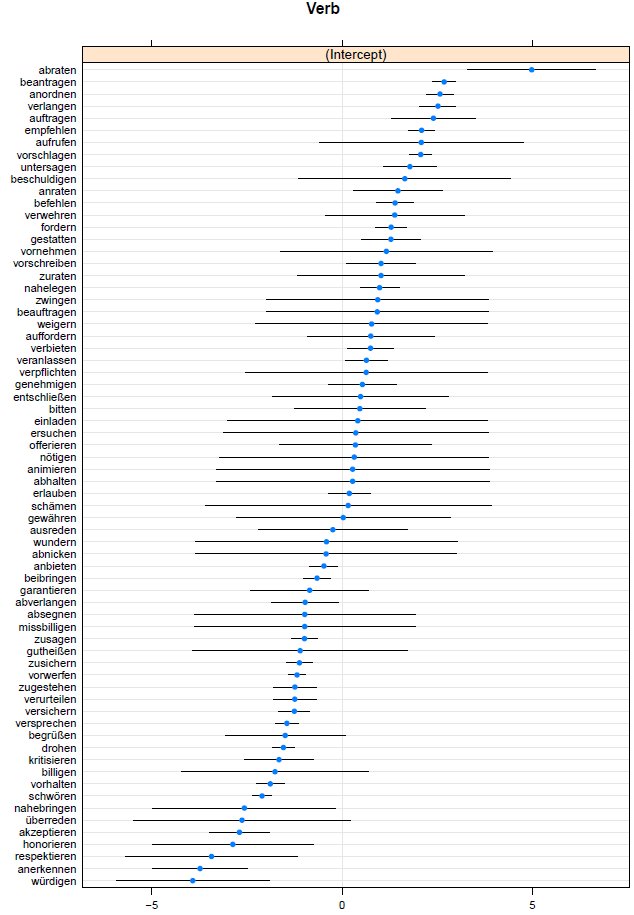
Abbildung 3 visualisiert den Randomeffekt. Dargestellt sind die vorhergesagten bedingten Modi der Gruppen (die individuellen Konstanten für die einzelnen Verblemmata), zusammen mit ihren 95%-Vohersageintervallen. Hierin spiegelt sich die Tendenz individueller Lemmata zur zu-Variante wider (ceteris paribus, je größer der geschätzte Koeffizient, desto höher die Wahrscheinlichkeit, einen zu-Infinitiv vorzufinden), zum anderen zeigt sich in den individuellen Konstanten auch die Menge an Evidenz, die für ein gegebenes Verblemma vorliegt (ceteris paribus liegen die Konstanten von weniger gut belegten Lemmata näher am Durchschnittswert aller Konstanten, 0). Die abgebildeten Intervalle spiegeln Unsicherheit in der Vorhersage wieder: Für häufig belegte Lemmata (z.B. beantragen, 343 Belege) kann die Konstante mit größerer Zuverlässigkeit vorhergesagt werden, als für schwach belegte Lemmata (z.B. einladen, 3 Belege).
Abbildung 3: Konditionale Modi (vorhergesagte Konstanten) für Verblemmata, mit 95%-Vorhersageintervallen
Modellevaluation - Pseudo-R2
Für klassische lineare Modelle lässt sich die Modellgüte mit Hilfe des R2-Werts beurteilen, der den Anteil der durch das Modell beschriebenen Varianz angibt. Für generalisierte lineare Modelle wie das oben dargestellte gibt es kein direktes Äquivalent zum R2-Wert. Aus diesem Grund wurden verschiedene Pseudo- R2 vorgeschlagen, die in ähnlicher Weise die durch das Modell erklärte Varianz beziffern. Es gibt keinen Konsens darüber, welches dieser Maße zu bevorzugen ist (vgl. Long 1997, Menard 2000). Bei gemischten Modellen (wie dem oben beschriebenen) ergibt sich die zusätzliche Komplikation, dass ein Pseudo-R mit oder ohne Berücksichtigung der Randomeffekte berechnet werden kann. Nakagawa und Schielzeth (2013) schlagen ein zweifaches Pseudo-R2-Maß vor: Das marginale R2 ist ein Maß für die durch feste Effekte erklärte Varianz, und das konditionale R2 gibt die erklärte Varianz für das gesamte Modell an. Für das oben beschriebene Modell liegt das marginale R2 bei 0.59 und das konditionale R2 bei 0.82, d.h., die festen Effekte allein erklären einen beachtlichen Teil der Varianz, und durch die Modellierung der Varianz zwischen den Matrixverblemmata (der Randomeffekt) kann das Gesamtmodell einen Großteil der Varianz in den Daten erklären.
Vorhersagequalität
Ein weiteres Kriterium für die Modellevaluation ist die Vorhersagequalität. Das Modell sagt für jeden Fall eine Wahrscheinlichkeit für das Auftreten des zu-Infinitivs vorher. Diese Wahrscheinlichkeiten lassen sich auf diskrete Ereignisse (ein zu-Infinitiv tritt auf oder nicht) abbilden. Üblicherweise nimmt man dabei eine vorhergesagte Wahrscheinlichkeit von 0.5 als Schwellenwert. Die auf diese Weise vorhergesagten Fälle von zu-Infinitiven können mit den tatsächlichen Beobachtungen verglichen und der Anteil korrekt klassifizierter Fälle kann angegeben werden. Dieser Wert für sich genommen ist jedoch nicht sehr aussagekräftig, weil ein naives Modell schon mindestens 50% der Daten korrekt vorhersagen würde, wenn es immer die häufigere der beiden Kategorien auswählt. In unserem Datensatz kommen dass-Komplementsätze (51.39%) häufiger vor als Komplementierungen mit zu-Infinitiv.
Diese Baseline kann man berücksichtigen, indem man bei der Anteilsberechnung die Zahl der Fälle abzieht, die ein im obigen Sinne naives Modell korrekt klassifiziert hätte. Dieses Maß wird gelegentlich auch als R2CountAdjusted bezeichnet. Man erhält damit eine Einschätzung darüber, wie sich die zusätzlichen Prädiktoren im Model auf die Vorhersagegüte auswirken. Für das oben beschriebene Modell liegt dieser Wert bei 0.73 und ist damit relativ hoch.
Der Einfluss der Verbklasse
Als Alternative zum obigen Modell 1 lässt sich ein alternatives Modell 2 spezifizieren, das zusätzlich zu den bisher verwendeten Prädiktoren auch die Verbklasse mit einbezieht. Die Verbklasse fungiert dabei als Prädiktor auf der zweiten Ebene des hierarchischen Modells, d.h., sie stellt zusätzliche Information bereit, um die lemmaspezifische Konstante αj vorherzusagen. Modell 2 hat die Form:
Pr(zu = 1) = logit−1(αj + β0 + β1X1 + β2X2 + β3X3 + β4X4)
mit
αj ~ N (γ0 + γ1 X5, σα2)
Wie zuvor ist dabei αj die Konstante für Verblemma j. Im Unterschied zum einfacheren Modell 1 werden hier jedoch die αj durch eine Regression modelliert, die mit X5 (Verbklasse) einen weiteren Prädiktor beinhaltet. Tabelle 3 zeigt die Parameterschätzungen für Modell 2.
| Koeffizient | Standardfehler | p | |
| (Intercept) | −0.013 | 0.847 | 0.98745 |
| Koref = AO | 4.755 | 0.385 | < 2 ⠂ 10-16 |
| Koref = DO | 3.474 | 0.149 | < 2 ⠂ 10-16 |
| Koref = PK | 2.287 | 0.412 | 2.87 ⠂ 10-8 |
| Koref = SU | 4.584 | 0.167 | < 2 ⠂ 10-16 |
| K.Modal = 1 | −4.189 | 0.198 | < 2 ⠂ 10-16 |
| K.Passiv = 1 | −4.258 | 0.352 | < 2 ⠂ 10-16 |
| Reflex = 1 | −0.047 | 0.229 | 0.83804 |
| Klasse = DO-K | −0.981 | 0.937 | 0.29519 |
| Klasse = A-K | −3.132 | 1.005 | 0.00183 |
| Klasse = SU-K | −3.040 | 1.074 | 0.00464 |
Tabelle 3: Mehrebenenmodell mit Verbklasse als zusätzlichem Prädiktor für die lemmaspezifischen Konstanten; die Ausprägung AO-K (Akkusativobjektkontrollverb) liegt auf dem Intercept
Auffällig sind die relativ hohen Standardfehler bei den geschätzten Koeffizienten für die Verbklasse. Bei Modell 2 liegt Nakagawa und Schielzeths Pseudo R2 für die festen Effekte deutlich über dem des einfacheren Modells (marginales R2 = 0.65), für das gesamte Modell einschließlich des Randomeffekt fällt die Steigerung sehr gering aus (konditionales R2= 0.83). Häufig werden für die Entscheidung, ob ein Prädiktor in ein Modell aufgenommen werden soll oder nicht, Informationskriterien herangezogen, die bekanntesten sind Akaikes Informationskriterium (AIC, Akaike 1973) und das Bayesische Informationskriterium (BIC; Schwarz, 1978), sowie Varianten davon. Informationskriterien setzen die Modellanpassung in Beziehung zur Modellkomplexität, d.h. eine möglicherweise verbesserte Modellanpassung wird abgewogen gegen eine höhere Modelkomplexität durch zusätzliche Prädiktoren. Wie Tabelle 4 zeigt, würden in unserem Fall beide Informationskriterien dagegen sprechen, die Verbklasse als Prädiktor ins Modell aufzunehmen.
| AIC | BIC | |
| Modell 1 (ohne Klasse) | 4903 | 4979 |
| Modell 2 (mit Klasse) | 4916 | 4987 |
Tabelle 4: Modellvergleich anhand von Akaikes Informationskriterium (AIC) und des
Bayesischen Informationskriteriums (BIC). Nach beiden wäre hier das weniger komplexe Modell (ohne
Verbklasse als Prädikator) zu bevorzugen.
Darüber hinaus lässt sich ein Modell 3 spezifizieren, das auf Koreferenz als Prädiktor verzichtet und die Verbklasse als Prädiktor beibehält:
Pr(zu = 1) = logit−1(β0 + β1X1 + β2X2 + β3X3 + β4X4)
mit
αj ~ N (γ0 + γ1 X5, σα2)
Nach allen bisher verwendeten Maßen liegt die Modellgüte von Modell 3 deutlich unter Modell 1 und Modell 2, die Koreferenz als Prädiktor mit einbeziehen (R2marginal = 0.52, R2konditional = 0.74, R2CountAdjusted = 0.55).
Rolle der lemmataspezifischen Konstanten
Um die Rolle der variablen Konstanten in den bisher berechneten gemischten Modellen zu illustrieren, lässt sich ein generalisiertes lineares Modell 4 spezifizieren, bei dem nur eine einzige Konstante geschätzt wird (statt, wie bei den bisher betrachteten gemischten Modellen, eine Konstante für jedes Verblemma vorherzusagen). Die restlichen Prädiktoren entsprechen dabei wie in Modell 1 KOREF, K.MODAL, K.PASSIV und REFLEX:
Pr(zu = 1) = logit−1(β0 + β1X1 + β2X2 + β3X3 + β4X4)
Das R2CountAdjusted dieses Modells liegt mit 0.65 deutlich unter dem der beiden Modelle mit variablen Konstanten für Verblemmata (R2Nagelkerke = 0.58). Auch ein fünftes Modell, das zusätzlich noch die Verbklasse berücksichtigt, weist kein verbessertes R2CountAdjusted auf (R2Nagelkerke = 0.6).
In den bisher spezifizierten Modellen wurde die syntaktische Funktion des koreferierenden Elements im Matrixsatz berücksichtigt. Es zeigt sich jedoch, dass dadurch nicht allzuviel gewonnen wird, d.h. ein alternatives Modell 6, das diese Unterscheidungen aufgibt und lediglich die Ausprägungen Koref=1 und Koref=0 umfasst, erklärt die Daten nur unwesentlich schlechter (marginales R2 = 0.59, konditionales R2 = 0.81, R2CountAdjusted = 0.73).
Zusammenfassung
Aus der obigen Diskussion geht hervor, dass erwartungsgemäß Koreferenz die entscheidende Rolle für die Wahl zwischen zu- und dass-Komplementierungen spielt. Darüber hinaus verhalten sich verschiedene Verblemmata recht unterschiedlich. Modelliert man diese Variabilität zwischen den Lemmata, indem man eine individuelle Konstante für jedes Verblemma zulässt und als Randomeffekt modelliert, verbessert sich die Vorhersagequalität deutlich. Wenn Variation zwischen Verblemmata auf diese Weise erfasst wird, leistet die Verbklasse als zusätzlicher Prädiktor wenig für die Modellierung der zu/dass-Alternation.