Evaluation des Entscheidungsbaums
Im Folgenden werden die Evaluationsmaße für einen Entscheidungsbaum mit zehnfacher Kreuzvalidierung und einem Stoppkriterium von mindestens zwei Fällen pro Blatt dargestellt. Der im Interpretationsabschnitt präsentierte Baum ist aus Gründen der Interpretierbarkeit mit einem groberen Stoppkriterium trainiert (ein Blatt muss dort mindestens 500 Fälle umfassen) und aus Gründen der Übersichtlichkeit vereinfacht.
Tabelle 6 gibt eine Übersicht über die Evaluationsmaße Genauigkeit (Precision), Trefferquote (Recall) und F-Maß (F-Score) für den auf allen Erstglied-Zweitglied-Folgen trainierten Entscheidungsbaum. Wenn die Erstglied-Zweitglied-Folge ein variables Fugenelement hat, werden alle Fälle als korrekte Vorhersage gewertet, die mindestens eins der möglichen Fugenelemente vorhersagen. Wenn also das Fugenelement ‚s’ oder ‚0’ (=Null-Fuge) sein kann, so werten wir die drei Voraussagen ‚s’, ‚0’ und ‚[var_0_s]’ als korrekt. Insgesamt werden durchschnittlich 95% der Testdaten korrekt klassifiziert, vgl. Tabelle 6 (F-Maß). Die häufigsten Fugen, die Null- und die s-Fugen, werden in 97% bzw. 96,5% der Fälle korrekt vorausgesagt, die ebenfalls häufige n- und en-Fugen allerdings nur zu 89 bzw. 87% der Fälle. Besonders schlecht wird die Tilgung von e (z.B. in Mietwohnung; Miete + Wohnung) vorausgesagt (65%).
Tabelle 6 zeigt darüber hinaus auch die Verteilung der Komposita auf die unterschiedlichen Fugenelemente. Obwohl die Verteilung tendenziell anderen Analysen ähnelt (vgl. für eine Übersicht Donalies 2011, S. 32), gibt es Differenzen, die mit den unterschiedlichen Korpuszusammensetzungen und Berechnungs- bzw. Erhebungsmethoden zusammenhängen. Insbesondere die Unterschiede zur Verteilung, die in Donalies (2011, S. 32) dargestellt ist und die eigentlich auf die gleiche Datenbasis zurückgeht, können auf die differierenden Auswahlkriterien der vorliegenden Studie zurückgeführt werden. So berücksichtigten wir nur zweigliedrige Komposita, deren Glieder in CELEX vorhanden sind (vgl. Kapitel "Datenaufbereitung"). Gleichwohl zeigt sich auch in unseren Daten, dass die Null-Fuge den größten Anteil ausmacht, gefolgt von der s- und der (e)n-Fuge.
| Fugenelement | Anzahl Fälle | Anteil in % | Genauigkeit | Trefferquote | F-Maß |
| 0 | 247.217 | 60,61% | 0,976 | 0,976 | 0,971 |
| s | 87.186 | 21,38% | 0,953 | 0,979 | 0,965 |
| n | 37.933 | 9,30% | 0,843 | 0,933 | 0,866 |
| en | 10.752 | 2,64% | 0,910 | 0,830 | 0,868 |
| variables Fugenelement | 7.985 | 1,96% | 0,952 | 0,979 | 0,966 |
| -e (=Tilgung des e) | 6.874 | 1,69% | 0,725 | 0,582 | 0,646 |
| es | 3.076 | 0,75% | 0,648 | 0,922 | 0,761 |
| er | 2.906 | 0,71% | 0,829 | 0,712 | 0,766 |
| e | 2.504 | 0,61% | 0,729 | 0,749 | 0,739 |
| um --> en | 1.113 | 0,27% | 0,975 | 0,980 | 0,978 |
| nen | 167 | 0,04% | 0,906 | 0,982 | 0,943 |
| ns | 152 | 0,04% | 0,849 | 1,000 | 0,918 |
| alle | 407.865 | 100,00% | 0,941 | 0,958 | 0,950 |
Tabelle 6: Evaluationsmaße für den ersten Entscheidungsbaum aufgeteilt
nach Fugenelement
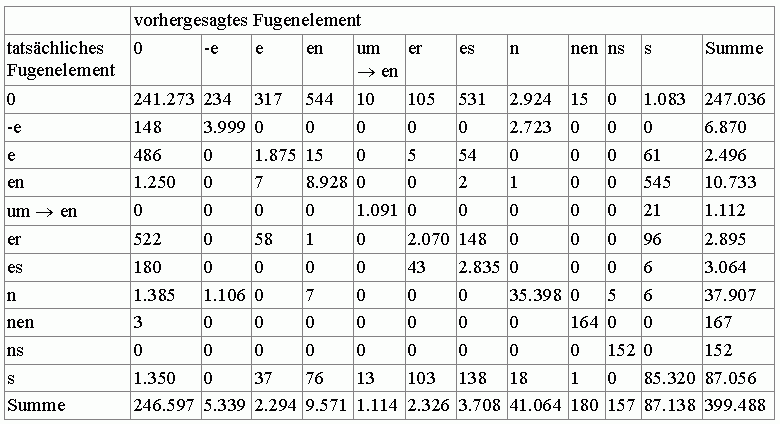
Doch nun zurück zu den Daten der Evaluation: Einen besseren Überblick über die problematischen Voraussagen bieten Konfusionsmatrizen. Sie stellen im vorliegende Fall dar, welche Fugenelemente vorausgesagt und welche Fugenelemente in den Komposita dann tatsächlich gefunden wurden.
Tabelle 7: Konfusionsmatrix vorhergesagte vs. tatsächliche Fugenelemente
In der Diagonalen von Tabelle 7 ist erwartungsgemäß ersichtlich, dass in den meisten Fällen das vorhergesagte auch dem tatsächlichen Fugenelement entspricht.1 Es sind aber auch die kritischsten Verwechslungen sichtbar: So wird für eine Null-Fuge oder eine e-Tilgung des Erstglieds oft stattdessen eine n-Fuge oder statt einer Null-Fuge fälschlicherweise eine s-Fuge vorausgesagt.2 Und umgekehrt sind vorausgesagte Null-Fugen in den Daten oft n-, s-, en-, er- oder e-Fugen.
Wie bereits erwähnt, haben wir für die linguistische Interpretation nicht mit dem kompletten Entscheidungsbaum gearbeitet, da dieser viel zu komplex ist, um daraus linguistisch sinnvolle Regeln abzuleiten. Der im Folgenden interpretierte Baum umfasst pro Blatt mindestens 500 Fälle und wurde im Prozess der Interpretation so zurückgeschnitten, dass sich linguistisch beschreibbare Zusammenhänge erkennen lassen.
Das hat zur Folge, dass der so zurückgestutzte Baum auch nicht mehr 95% der Komposita
voraussagen kann, sondern – wie weiter unten detailliert ausgeführt werden wird – etwa
75%.
1 Die Konfusionsmatrix umfasst nur diejenigen 399.488 Fälle, in denen das Fugenelement nicht variabel ist. [zurück]
2 Die Voraussage der n-Fuge statt der korrekten e-Tilgung des Erstglieds war bereits oben in Tabelle 6 sichtbar, wo wir feststellten, dass die Tilgung von e generell schlecht vorausgesagt wird. Das statistische Modell würde also z.B. im Fall von Mietwohnung aufgrund der linguistischen Merkmale der Glieder eher davon ausgehen, dass es Mietenwohnung heißen müsste. [zurück]