Konnektoren und Funktor-Argument-Struktur

In der Semantik geht man davon aus, dass die Interpretationen einfacher und komplexer Ausdrücke nach denselben Prinzipien strukturiert sind. Eine verbreitete Hypothese bedient sich dabei der Strukturierung von Ausdrücken in Funktoren und ihre Argumente, die einander in einer Funktion zugeordnet sind.

Prädestiniert für die Rolle als Argumente sind die Bedeutungen von Ausdrücken, welche Individuen bezeichnen, vor allem von Personalpronomina, etwa anaphorischen Personalpronomina oder Kommunikanten-Pronomina, von Eigennamen und Nominalphrasen. So sind die Ausdrücke Er, Hans und der faule Kerl Argument des Funktors, der durch schläft ausgedrückt wird:

Auch Propositionen kommen als Argumente von Funktoren vor:

Je nach der Zahl ihrer möglichen Argumente weisen die Funktoren Leerstellen für ihre Argumente auf.

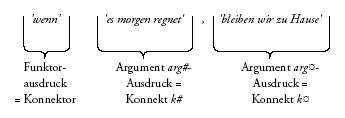
Es hat sich in der Literatur eingebürgert, in semantischen Beschreibungen diese Leerstellen durch den griechischen Buchstaben λ (lambda) anzuzeigen. Die Leerstellen werden durch Variablen verschiedener Sorten (Individuenvariablen, d.h. Variablen über Personen und Gegenstände: x und y , oder Propositionenvariablen, d.h. Variablen über Propositionen: p und q) repräsentiert. Diese können bei der Verwendung des jeweiligen Funktorausdrucks gemäß syntaktischer Regeln und damit verknüpften semantischen Interpretationsregeln durch die Denotate anderer Ausdrücke ersetzt ("belegt") werden, die vom selben semantischen Typ und derselben Sorte sind wie die Variablen. So werden in dem Satz

die beiden Argumentstellen λp und λq der Bedeutung λpλq ['wenn' (p,q)] von wenn durch die Denotate der Ausdrucksketten es morgen regnet (für p) und bleiben wir zu Hause (für q) belegt. Die betreffenden Denotate fungieren dann als Konstante.

Durch die Belegung sämtlicher Argumentleerstellen eines durch ein Verb, Partizip I bzw. II, Adjektiv oder Nomen ausgedrückten Funktors wird eine Proposition konstituiert.

Die Anzahl der Argumentvariablen eines Funktorausdrucks gibt an, wie viele Konstante als Argumente des betreffenden Funktors fungieren können. Sie macht die Stelligkeit des Funktors und auch seines Ausdrucks aus. So ist die Bedeutung des Adverbs vielleicht, das Sachverhalten eine epistemische, also auf ihre Geltung als Tatsache oder Nicht-Tatsache bezogene Bewertung zuschreibt, ein einstelliger Funktor.

Dabei bezeichnet das unmittelbar auf wenn folgende Konnekt k# das interne Konnekt des Konnektors, das andere Konnekt ist das externe Konnekt des Konnektors. Ausgenommen von dieser Zweistelligkeit sind Konnektoren vom Typ der Pronominaladverbien und Relativadverbien wie dagegen und wohingegen: Hier ist eines der Argumente der Funktion im Konnektor durch die deiktische da- bzw- wo-Komponente selbst ausgedrückt, die im externen Konnekt ein korrefentes Argument hat.

Das, was das Argument eines Funktors bildet, nennen wir seinen Skopus. Bei mehrstelligen Funktoren besteht der Skopus aus mehreren Argumenten. So bilden bei Konnektoren beide Argumente zusammen den Skopus des Konnektorbedeutung. Davon zu unterscheiden ist ihr semantischer Bereich, der die Bedeutung des internen Konnekts umfasst. Das interne Konnekt, das syntaktisch enger mit dem Konnektor verknüpft ist als sein externes Konnekt, bildet den syntaktischen Bereich des Konnektors.

Bei Subjunktoren bildet der komplexe Ausdruck aus Konnektor und internem Konnekt wiederum einen komplexen Funktorausdruck, der auf das externe Konnekt angewandt wird.

Funktoren stellen Anforderungen an den semantischen Typ ihrer Argumente: Das allgemeine Konnektorenmerkmal 'Relate bezeichnen Sachverhalte' legt fest, dass als Argumente von Konnektoren nur Ausdrücke für Propositionen, sogenannte propositionale Strukturen, in Frage kommen. Diese propositionalen Strukturen werden prototypisch durch vollständige Sätze ausgedrückt. Es können aber auch Strukturen sein, die Ergebnisse von Weglassungen aus Sätzen sind. Siehe Satzstrukturen als Konnekte. Wir nennen die möglichen Argumente von Konnektoren zusammenfassend Satzstrukturen bzw. Satzstrukturbedeutungen.